Notation

• ${\rm CH(Q)}$ represents convex hull

Graham’s Scan $O(n\lg n)$

It solves convex-hull problem by maintaining a stack $S$ of candidate points. It pushes each point of the input set $Q$ onto the stack one time, and it eventually pops from the stack each point that is not a vertex of ${\rm CH}(Q)$.

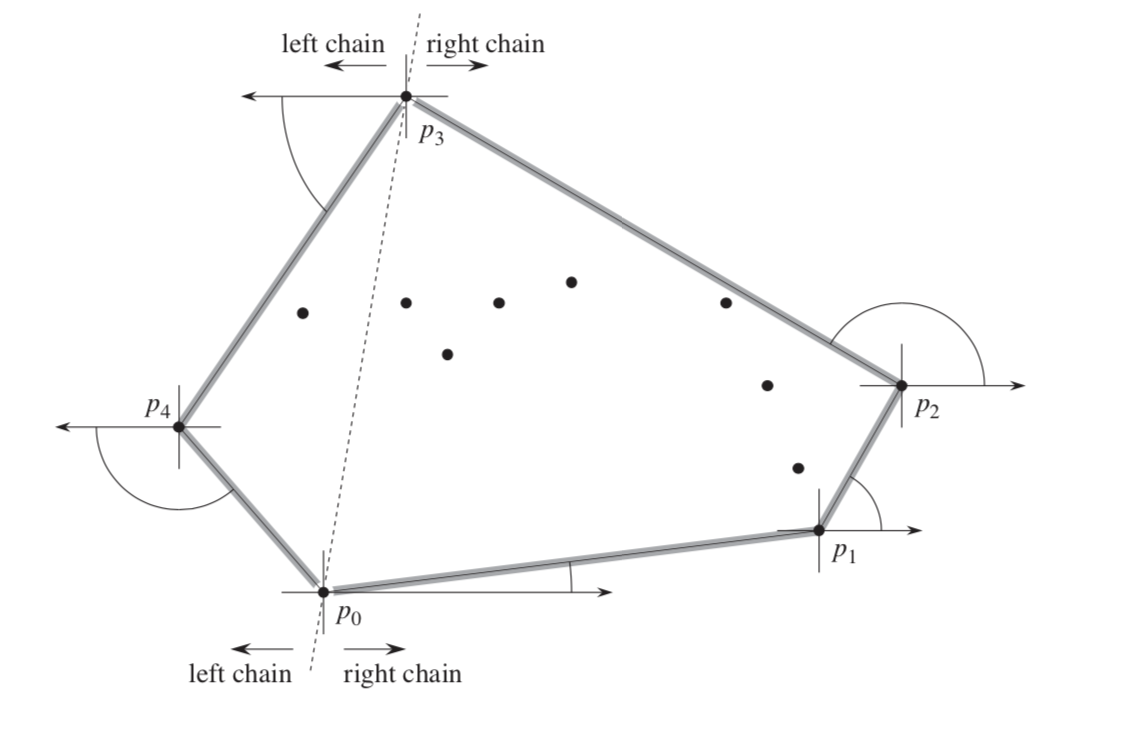
• $p_0$ is the point in $Q$ with th eminimum $y$-coordinate (leftmost in case of tie)
• $\langle p_1, p_2,…p_m\rangle$ remaining points in $Q$ sorted by polar angle in counterclockwise order around $p_0$, (take farthest in case of tie.)
• $S=\langle p_0, p_1, p_2\rangle$ (pop from right side, $p_2$ first)
• For point $p_i=p_3$ to $p_m$
  • While angle formed by points second and first element of $S$ make a nonleft turn: Remove top elemnt.
  • push $p_i$ to $S$
• Finally, $S={\rm CH(Q)}$

Jarvis’ March $O(nh)$

[Here $h$ is the number of vertices in ${\rm CH(Q)}$, where $h$ is $o(\lg n)$]

We start from lowest point $p_0$ and take the point with smallest polar angle wrt $p_1$. Then we take $p_2$ with the smallest poisitive angle wrt $p_1$ and so on until we reach the highest point $p_k$, then we do the same but we calculate the angle from negative x-axis. Finally we reach back at $p_0$.