Selection algorithm SELECT for finding the $i^{\rm th}$ smallest element:

  1. Divide the array into $\lfloor n/5\rfloor$ groups of 5 elements each (last one has $n\mod 5$). $O(n)$

  2. Find the median of each of the groups by insertion-sorting the elements of each group and picking the median from the sorted list of group elements. $O(n)$

  3. Use SELECT recursively to find the median $x$ of the $\lceil n/5\rceil$ medians found. $T(\lceil n/5\rceil)$

  4. Partition the array into $L$ & $R$ based on $x$. Let $k=\vert L\vert + 1$. Note that $x$ is $k^{\rm th}$ smallest element and there are $n-k$ elements in $R$. $O(n)$
  5. Based on $i$:
    1. $i=k$, return $x$.
    2. $i<k$, recurse SELECT on $L$ for $i$
    3. $i>k$, recurse SELECT on R for $i-k$

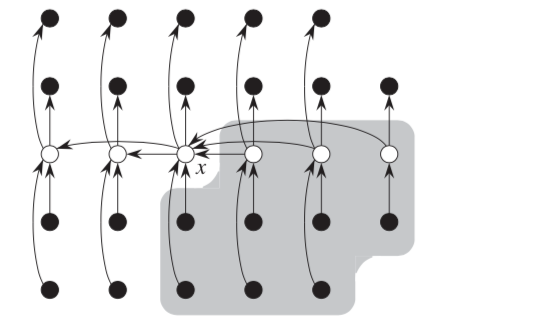
We see that atleast $1/2$ of the medians found in 2 are greater than or equal to medians-of-medians $x$. Thus atleast half of the $\lceil n/5\rceil$ groups contribute atleast 3 elements that are greater than $x$, except for the last one and the group containing $x$ itself.Thus number of elements greater than $x$ is at least:

$\displaystyle 3\left(\left\lceil\frac 12\left\lceil\frac n5\right\rceil\right\rceil-2\right)\ge \frac {3n}{10}-6$

Thus in worst case step 5 calls SELECT recursively on atmost $7n/10+6$ elements. \(\begin{align} T(n)&\le cn+T(n/5)+T(7n/10)\\ &\le cn + \left(c\frac n5+T(n/5^2)+T(7n/50)\right)+\left(c\frac {7n}{10}+T(7n/50)+T(7^2n/10^2)\right)\\ &= cn + 9\frac {cn}{10} + T(n/5^2) + 2T(7n/50) + T(7^2n/10^2)\\ &\le \ldots\\ &\le \sum_{i=0^h}\left(\frac {9}{10}\right)^icn+\ldots\\ &\le cn\frac 1{1-9/10} = O(n) \end{align}\)

Max height of tree is $(7/10)^h\le 1\implies h\ge \log_{10/7}n$.