Theorem: (T(n)=aT(\lceil n/b\rceil)+O(n^d)) for some constants (a>0,b>1,d\ge 0) then \(T(n)=\begin{cases} O(n^d)&d>\log_b a\\ O(n^d\log n)&d=\log_ba\\ O(n^{\log_ba})&d<\log_ba \end{cases}\)

Proof: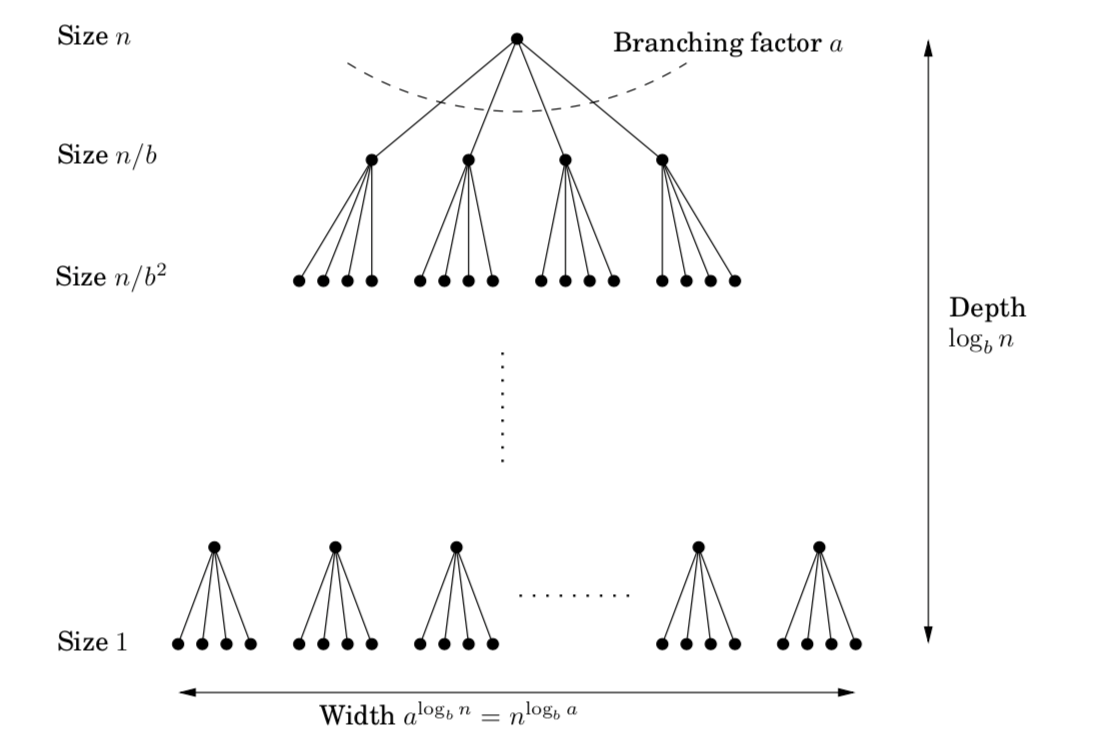

Each problem of size (n) is divided into (a) subproblems of size (n/b). Each level has problem of size (n/b^k) and work done is: \(a^k\times O\left(\frac nb^k\right)^d=O(n^d)\times \left(\frac ab^d\right)^k\)

As (k) goes from (0) (root) to (\log_bn) (the leaves), these form a geometric series with ratio (r=a/b^d)

  1. (r<1): Decreasing series, sum is first term (O(n^d))
  2. (r>1): Increasing series, sum is last term (O(n^{\log_ba}))
\[n^d\left(\frac a{b^d}\right)^{\log_bn}=n^d\left(\frac{a^{\log_bn}}{(b^{\log_bn})^d}\right)=a^{\log_bn}=a^{(\log_an)(\log_ba)}=n^{\log_ba}\]
  1. (r=1): All (O(\log n)) terms are equal to (O(n^d))