Procedure	Binary Heap	Binomial Heap (worst case)	Fibonacci Heap (amortized)
Make Heap	(\Theta(1))	(\Theta(1))	(\Theta(1))
Insert	(\Theta(\lg n))	(O(\lg n))	(\Theta(1))
Minimum	(\Theta(1))	(O(\lg n))	(\Theta(1))
Extract Min	(\Theta(\lg n))	(\Theta(\lg n))	(\Theta(\lg n))
Union	(\Theta(n))	(O(\lg n))	(\Theta(1))
Decrease Key	(\Theta(\lg n))	(\Theta(\lg n))	(\Theta(1))
Delete	(\Theta(\lg n))	(\Theta(\lg n))	(\Theta(\lg n))

Binary Heap

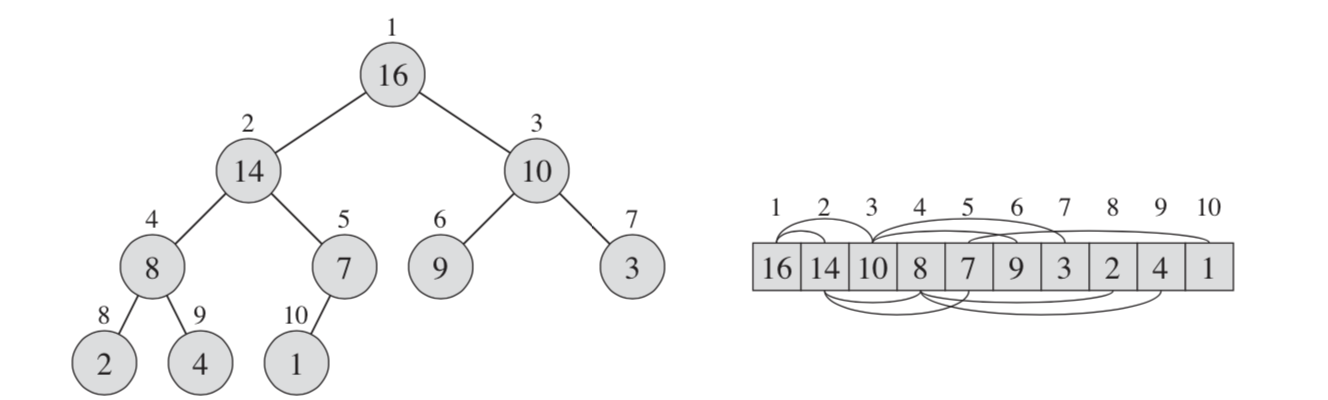
A binary heap is an array object which we can view as a nearly complete binary tree with pointers as follows:

Parent: (\lfloor i/2\rfloor)
Left child: (2i)
Right child: (2i+1)

These satisfy the heap property, i.e. for max-heap (A[{\rm Parent}(i)]\ge A[i]) or vice versa for min-heap. A heap of height (h) can have nodes from (2^h)(1 node at last level) to (2^{h+1}-1)(full tree). So (h\le \lg n \le h+1) so (h=\lfloor \lg n\rfloor).

Heapify (O(h)=O(\lg n))

If binary tree at ({\rm Left}(i)) and ({\rm Right}(i)) satisfy the heap property but (A[i]) does not then we need to perform heapify operation. In max-heap we exchange (A[i]) with the largest of ({\rm Right}(i)) and ({\rm Left}(i)) and recursively perform heapify operation at the exchanged node (the new parent).

Building (O(n))

Elements from (\lfloor n/2\rfloor+1) to (n) are all leaves of the tree so each is a 1-element heap. We run heapify on rest of the elements in order from (\lfloor n/2\rfloor) to (1). Total time taken for height (i) is (2^i\cdot O(h-i)). Sum over all levels is \(O(\sum_{i=0}^{\lg n} 2^{h-i}.i) =O\left(\sum _{i=0}^{\lg n}2^h . \frac i{2^i}\right)=O\left(n\cdot\sum_{i=0}^{\lg n}\frac i{2^i}\right)=O(n)\) Where (\sum_{x=0}^\infty x/2^x=x/(1-x)^2) and we put (x=1/2) to get (\sum i/2^i\le 2).

Extract Min (O(\lg n))

Replace min value with last element and perform heapify after removing the min element.

Binomial Heap

A binomial tree (B_k) is defined recursively consisting of two (B_{k-1}) linked together.

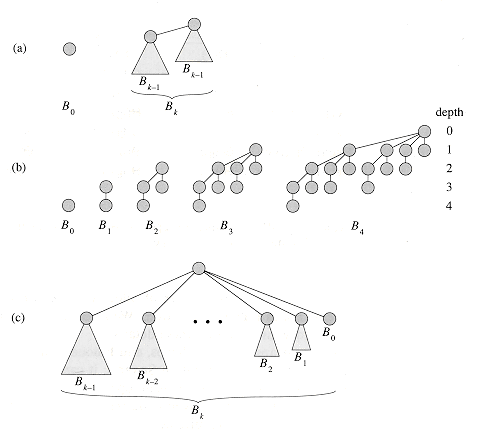
A tree (B_k)

Contains (2^k) nodes
has height (k)
there are (k \choose i) nodes at depth (i) (which gives it the name binomial heap)
root has degree (k)

A binomial heap (H):

Each binomial tree is heap ordered.
there is atmost 1 tree whose root has a given degree.

So a binomial heap (H) has atmost (\lfloor\lg n\rfloor+1) binomial trees (from binary representation)

Finding Min (O(\lg n))

See the roots of all (O(\lg n)) trees.

Uniting two binomial heaps (O(\lg n))

For merging two binomial trees (B_{k-1}) with roots (y) and (z) we would make (z) parent of (y) and make the child of (z) sibling of (y). This takes (O(1)) time.

For merging two heaps we would do the same as binary addition. This would take (O(\lg n)) time as there are atmax (\lg n) trees.

Inserting a node (O(\lg n))

Create (B_0) with the node and perform heap union.

Extracting Min (O(\lg n))

Merge the children of the tree with minimunm key with the rest of the trees.

Decreasing a key (O(\lg n))

Change key value and perform heapify operation.

Deleting a key (O(\lg n))

Decrease key to (-\infty) and extract min.

Fibonacci Heap

A Fibonacci heap is a collection of trees that are heap-ordered connected in a circular, doubly linked list. Each node may also be marked. We also store the minimum of the heap using a separate pointer.

Suppose

At some time, (x) was a root.
then (x) was linked to (made child of) another node
then two children of (x) were removed by cut operation

As soon as second child has been lost we remove (x) from it’s parents making it a new root. (x.{\rm mark}) is true if steps (1) and (2) have occured and one child of (x) has been cut.

Note: Maximum degree of a node is (D(n)\le \lfloor\log_{\phi}n\rfloor) where (\phi) is the golden ration (\phi=(1+\sqrt 5)/2). Hence (D(n)\le O(\lg n))

Potential

(t(H)) represents the number of trees in heap (H) and (m(H)) represents the number of marked nodes in (H). We define the potential of (H) as (\phi(H)=t(H)+2m(H))

Create a new heap (O(1))

Just allocate empty heap (H) with (0) trees and NULL min pointer (\phi(H)=0)

Insert a node (O(1))

Just insert the node in the root list and update min-pointer if necessary. (\Delta\phi(H)=1)

Finding the min (O(1))

Return the value pointed by min pointer. (\Delta \phi(H)=0)

Uniting two fibonacci heaps (O(1))

Concatenate two root lists and update min-pointer if necessary. \(\begin{align}\Delta\phi(H)&=\phi(H)-\phi(H_1)-\phi(H_2)\\&=(t(H)+2m(H))-((t(H_1)+2m(H_1))+(t(H_2)+2m(H_2))) \\&=0\end{align}\)

since (t(H)=t(H_1)+t(H_2)) and (m(H)=m(H_1)+m(H_2))

Extracting the min node (O(\lg n))

Add the children of tree whose root is pointer by min-pointer to the root list of (H) and then remove it from the root list. Also update min pointer. This takes (O(D(n))). Then consolidate the root list by linking roots of equal degrees until atmost one root remains of each degree. To link (y) and (x) remove (y) from root list of (H) and make (y) child of (x) and unmark (y) is previously marked (step 2).

The above operation will increate elements in root list to at most (D(n)+t(H)-1), original (t(H)) minus (1) extracted node, new (D(n)) children of extracted node. The total time taken for combining roots is therefore atmost (O(D(n)+t(H))).

The potential before is (t(H)+2m(H)) and afterwards at most ((D(n)+1)+2m(H)). Thus amortized cost is \(\begin{align} &O(D(n)+t(H))+((D(n)+1)+2m(H))-(t(H)+2m(H))\\ &=O(D(n))+O(t(H))-t(H))\\ &=O(D(n)) \end{align}\)

Decreasing a key (O(1))

Cut the link between the node (x) with the key and it’s parent (y), making (x) the root (also unmark it if marked, step 1). This is a cut operation. Then perform a cascading cut where:

If (y) is unmarked then mark it (since it has lost it’s first child)
Else perform cut operation at (y) and perform cascading cut at (y)’s parent.

This goes on until a unmarked node or root is found. Finally we update the min-pointer. Total time taken is (O(1)) for decreasing key, (O(c)) for cascading cuts consisting of (c) total cuts.

For change in potential:

Cutting (x) from (y) creates a new tree rooted at (x) and clears (x)’s mark bit.
Each call of the cascading cut except for the last one cuts a marked node and clears the mark bit. Finally fibonacci heap contains (t(H)+c) trees ((t(H)) original, (c-1) from cascading cuts and (1) from (x)) and at most (m(H)-c+2) marked nodes ((m(H)) original, (c-1) unmarked from cascading cuts except last one which marked (1) node).

(((t(H)+c)+2(m(H)-c+2))-(t(H)+2m(H))=4-c)

Thus total amortized time taken is (O(c)+4-c=O(1))

1 unit of potential pays for (i) cut and clearing the mark bit. (ii) decrease in potential due to node (y) becoming a root.

Deleting a key (O(\lg n))

Decrease key to (-\infty) and extract min.