Motivation

Given a set of intervals $I$ on the real line and a query point $q_x$, find the intervals that contain $q_x$.

Let $I:={[x_1:x_1’],[x_2:x_2’],\ldots,[x_n:x_n’]}$. Let $x_{\rm mid}$ be the median of the $2n$ interval endpoints such that atmost half of them lie on the left and half of them lie on the right.

Definition

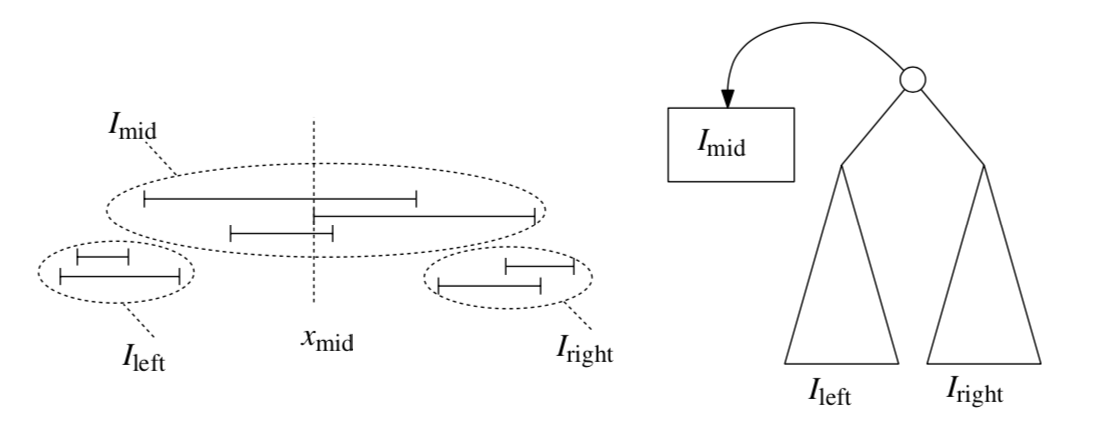
• If $I=\phi$ then interval tree is a leaf.
• Otherwise let $x_{\rm mid}$ be the median of the endpoints of the interval. Let
  • $I_{\rm left}:={[x_j:x_j’]\in I\mid x_j’<x_{\rm mid}}$
  • $I_{\rm mid}:={[x_j:x_j’]\in I\mid x_j\le x_{\rm mid}\le x_j’}$.
  • $I_{\rm right}:={[x_j:x_j’]\in I\mid x_j>x_{\rm mid}}$

The Interval tree consists of a root node $v$ storing $x_{\rm mid}$.

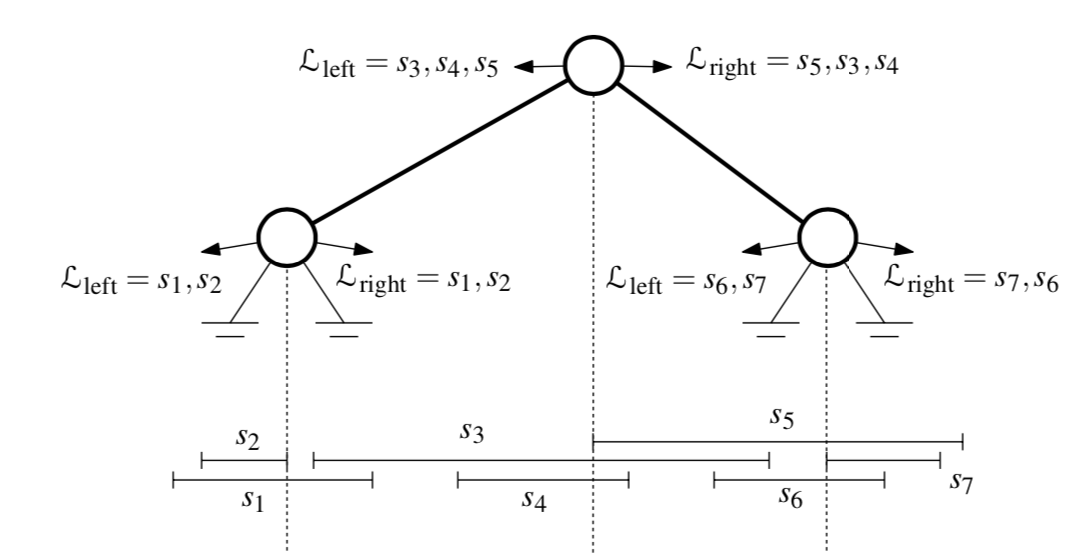
• $I_{\rm mid}$ is stored twice:

  1. ${\cal L}_{\rm left}$ that is sorted on the left endpoints of $I_{\rm mid}$

  2. ${\cal L}_{\rm right}$ that is sorted on the right endpoints of $I_{\rm mid}$

• Left subtree of $v$ is an interval tree for the set $I_{\rm left}$.

• Right subtree of $v$ is an interval tree for the set $I_{\rm right}$.

Creation $O(n\log n)$

create(I)
  if I = null
    return empty leaf
  else
    create a node v
    computer x_mid (linear time, constant if presorted)
    store x_mid with v
    compute I_mid, L_left, L_right
    left_child(v) <- create(I_left)
    right_child(v) <- create(I_right)
    return v

Querying $O(\log n+k)$

• If $q_x < x_{\rm mid}(v)$ walk along $\cal L_{\rm left}$ reporting all intervals that contain $q_x$. Stop as soon as an interval doesn’t contain $q_x$. Query left subtree of $v$.
• Symmetrically do for $q_x>x_{\rm mid(v)}$

$k$ = Number of reported intervals.

2-D Range Tree

The data structure to store a a horizontal line segments is $\rm T$. If we want to create a 2-D range tree then instead of $\cal L_{\rm left}(v)$ and $\cal L_{\rm right}(v)$ we will store:

• A range tree $T_{\rm left}(v)$ on left endpoint segments in $I_{\rm mid}(v)$.
• A range tree $T_{\rm right}(v)$ on right endpoint segments in $I_{\rm mid}(v)$

At time of querying instead of walking along $\cal L_{\rm left}(v)$ and $\cal L_{\rm right}(v)$ we will perform a query in the range trees $\rm T_{left}(v)$ and $\rm T_{right}(v)$.

• Creation: $O(n\log n)$
• Querying: $O(\log^2n+k)$