Definition

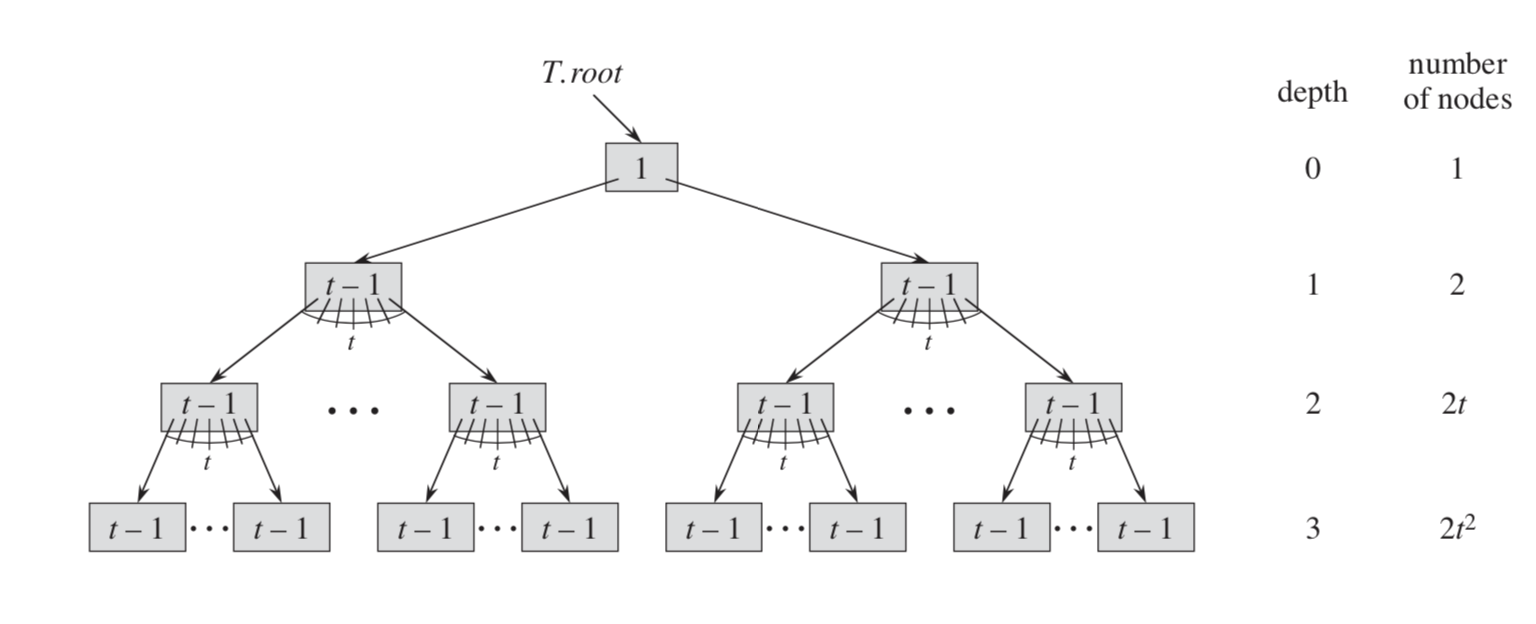
Figure: B-Tree of height 3 containing minimum number of keys

• Every node $x$ has $x.n$ keys and $x.n+1$ children (possibly undefined).
• The key $x.k_i$ separates the range of keys stores in children subtrees, say $l_i$ then $l_1\le x.k_1\le l_2\le x.k_2\le \ldots x.k_n \le l_{n+1}$
• All leaves have same depth
• Each node except root has $t-1$ keys to $2t-1$ keys. Therefore $t$ to $2t$ children.
• Height of tree $h=O(\log_tn)$

Operations

Search $O(th)=O(t\log_tn)$

• Find the subtree where given key exists using linear search
• recurse in that tree

Create $O(1)$

• Create a empty root node
• Insert keys

Insert $O(th)=O(t\log_tn)$

• Find the the leaf node by searching.
• If node is full split on median key to make two children nodes and insert the meadian key into parent node.

For single pass, split whenever you come across a full node while searching so as to be assured to no more split any nodes while shifting the median key upwards.

Splitting

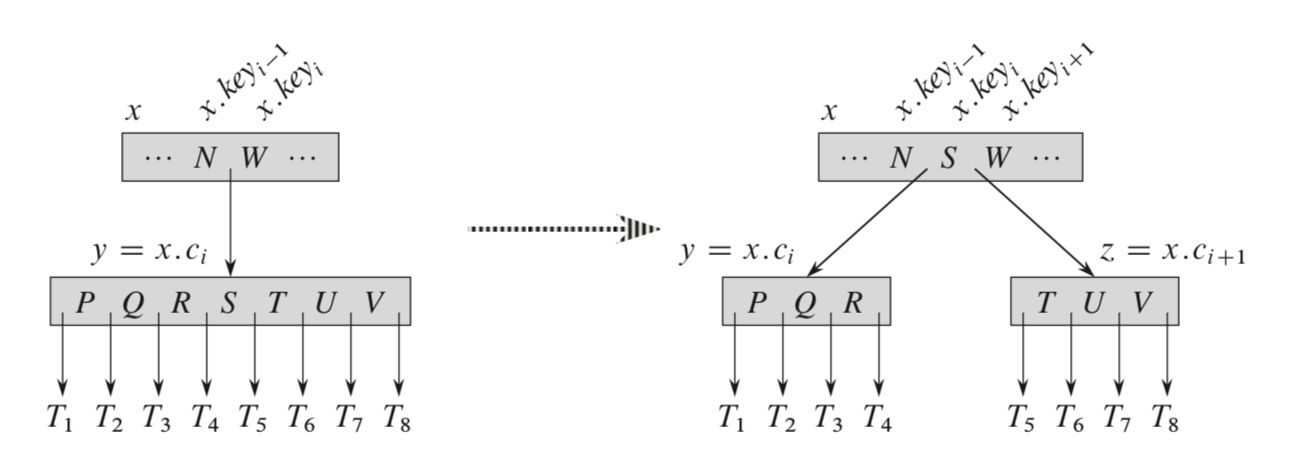
Figure: Splitting a node with $t=4$

• Make two nodes with keys less than and more than the median key respectively.
• Move the children between the keys to respective trees.
• Move the median key to parent node.
• Move the children around the median key to the left and right new nodes respectively.

Delete $O(th)=O(t\log_tn)$

• If key $k$ is in leaf node $x$ then delete $k$ from $x$.
• If key $k$ is in internal node $x$ then
  • If left child $y$ of $k$ has $\ge t$ keys then find predecessor $k’$ of $k$ in $y$. Delete $k’$ from $y$ and replace $k$ by $k’$ in $x$.
  • Otherwise check for right child $z$ and do symmetrically.
  • Otherwise merge $y$ and $z$ along with $k$ into $y$. Recursively delete $k$ from $y$.